Explorativní faktorová analýza

Základní pojmy

Explorativní faktorová analýza má za cíl analyzovat korelace většího množství měřitelných (manifestních) proměnných a na základě této analýzy určit skupiny proměnných, které statisticky „patří k sobě", tj. za kterými stojí společný faktor (latentní proměnná). Přitom počet nalezených faktorů by měl být co nejmenší a pozorované závislosti by měly být objasněny co nejjednodušeji. Poté, kdy faktor objevíme a pojmenujeme, můžeme z něj vytvořit novou proměnnou, kterou používáme v další analýze namísto původních položek.

Postup faktorové analýzy je založen na výběrových korelačních a parciálních korelačních koeficientech.
Korelační koeficient vyjadřuje těsnost lineární závislosti proměnných, pohybuje se v rozmezí -1 až 1.
Parciální korelační koeficient vyjadřuje těsnost lineární závislosti dvou proměnných, ovšem za předpokladu, že všechny ostatní proměnné jsou konstantní. Je-li možné závislost proměnných vysvětlit společnými faktory, musí být parciální korelační koeficienty, kde je tento vliv společných faktorů odrušen, velmi malé, v ideálním případě, kdy faktory vysvětlují lineární závislosti proměnných beze zbytku, nulové.

Reprodukovaný korelační koeficient vyjadřuje těsnost lineární závislosti dvou proměnných, které jsou vyjádřeny pomocí odhadnutých faktorů, tj. už na základě výsledků faktorové analýzy.

Reziduální korelační koeficient je dán rozdílem mezi pozorovaným a reprodukovaným korelačním koeficientem. Pokud nalezené faktory dobře vysvětlují korelace mezi manifestními proměnnými, měly by být reziduální korelační koeficienty malé, v ideálním případě nulové. Proto by reziduální korelační matice neměla chybět v žádné výstupní sestavě faktorové analýzy. Pro hrubé posouzení faktorového modelu můžeme například zkontrolovat, zda jsou všechny reziduální korelační koeficienty menší než např. 0,1. Pouhý pohled na rezidua není sice zcela spolehlivý, ale může leccos napovědět. Pokud např. vyšší hodnoty reziduálních korelačních koeficientů vytvářejí shluky, může to napovídat existenci dalších faktorů.

K tomu, abychom mohli faktorovou analýzu provést, potřebujeme mít k dispozici n pozorování každé z k manifestních proměnných X1 , X2 , X3 … Xk. Je třeba si uvědomit, že postup faktorové analýzy nerealizujeme na zkoumaném základním souboru, ale pouze na výběru z tohoto souboru.  Proto budou analogicky výsledky faktorové analýzy pouze odhady skutečných faktorů. 

Existují-li mezi proměnnými X1 , X2 , X3 … Xk lineární závislosti, budou jejich korelační koeficienty v absolutní hodnotě velké. Pokud bude splněn i další předpoklad faktorové analýzy, že za závislostí proměnných stojí latentní společné proměnné – faktory, budou parciálních korelační koeficienty proměnných X1 , X2 , X3 … Xk velmi malé. Analyzovat matici korelačních a parciálních korelačních koeficientů, abychom zjistili, zda se zkoumané proměnné hodí pro faktorovou analýzu, je pracné a nespolehlivé. Proto se pro posouzení vhodnosti faktorové analýzy používají dva ukazatele.

Nejpoužívanějším je Kaiser-Meyer-Olkinova míra (KMO). Koeficient KMO může teoreticky nabývat hodnot mezi 0 a 1. To proto, že je dán podílem součtu druhých mocnin korelačních koeficientů ku součtu druhých mocnin korelačních a parciálních koeficientů. Pro hodnoty KMO platí následující tabulka

Tab. 1 Hodnocení koeficientu KMO

KMO	Hodnocení KMO
0,9 - 1	skvělý
0,8 - 0,9	vysoký
0,7 - 0,8	střední
0,6 - 0,7	nízký
0,5 - 0,6	špatný
Do 0,5	FA nemá smysl

Další možností, jak jednoduchým způsobem zjistit, zda jsou zkoumané proměnné vhodné pro faktorovou analýzu, je testovat nulovou hypotézu, že korelační matice daných proměnných je jednotková (tj. na diagonále má jedničky, jinde nuly). To znamená, že korelační koeficienty mezi proměnnými jsou nulové, není tedy splněn základní předpoklad pro použití faktorové analýzy. Pokud tuto nulovou hypotézu zamítneme, má faktorová analýza smysl. Pro test této nulové hypotézy se používá Bartlettův test sféricity. Při dostatečně velkém počtu pozorování dochází k zamítnutí nulové hypotézy i při relativně malých korelačních koeficientech mezi proměnnými. Proto je vhodnější používat koeficient KMO. Vede k tomu i skutečnost, že Kromě celkového koeficientu KMO lze spočítat KMO i pro jednotlivé proměnné, tj. nejen pro všechny korelační koeficienty, ale také pouze pro korelační koeficienty s danou proměnnou.

KMO pro jednotlivé proměnné můžeme nalézt v tzv. Anti-image matici, tj. v matici záporných parciálních korelačních koeficientů. KMO jednotlivých proměnných jsou uvedeny na diagonále této matice.

Výsledky explorativní faktorové analýzy nejsou jednoznačné. To je dáno tím, že existuje celá řada metod extrakce, rotace a výpočtu skóre faktorů.

Faktory jsou zpravidla konstruovány tak, aby byly stochasticky nezávislé, a proto i nekorelované. Stejně jako manifestní proměnné, jsou i faktory standardizované, tj. jejich střední hodnota je 0 a rozptyl 1. Na tomto místě třeba poznamenat, že je možné pracovat i nestandardizovanými proměnnými a jejich kovarianční maticí. V tomto textu se omezíme na standardizované proměnné.

Matematicky lze postup faktorové analýzy popsat jako vyjádření zkoumaných standardizovaných proměnných Xi pomocí lineární kombinace menšího počtu hypotetických faktorů Fj následovně

X_i = a_i1 F₁ + a_i2 F₂ + a_i3 F₃ +      + a_im F_m + e_i,                                                                             (1)

pro i = 1, 2, 3, …k, kde k je počet manifestních proměnných, m počet faktorů a ei specifická (jedinečná, chybová, reziduální) část proměnné Xi , o níž předpokládáme, že její korelace se všemi faktory je nulová. Přitom požadujeme m < n.
Nulové jsou i korelace jednotlivých jedinečností mezi sebou. Protože i faktory jsou konstruovány tak, aby spolu vzájemně nekorelovaly, lze rozptyl proměnné Xi vyjádřit vztahem

Var(X_i) = Var(a_i1 F₁ + a_i2 F₂ + a_{i 3}F₃ +      + a_im F_m + e_i)

             = Var(a_i1 F₁) + Var(a_{i 2}F₂) + Var(a_i3 F₃) +      + Var(a_im F_m) + Var(e_i).                         (2)

Protože jak manifestní, tak i latentní proměnné jsou standardizovány (tj. mají rozptyl roven 1), platí

Var(X_i) = a_i1² + a_i2² + a_i3² +      + a_im² +Var(e_i) = 1.                                                                    (3)

Konstanty aij se nazývají faktorové zátěže. Nabývají hodnot mezi -1 a +1 a lze je interpretovat jako korelační koeficienty mezi pozorovanými proměnnými a faktory. Matici faktorových zátěží se říká faktorová matice. Součet druhých mocnin faktorových zátěží a_i1² + a_i2² + a_i3² +      + a_im²je roven části variability proměnné Xi vysvětlené všemi faktory Fj. Tento součet se nazývá komunalita proměnné. Komunalita proměnné je tedy ta část variability proměnné, která je vysvětlena faktory. Maximální možná hodnota komunality je rovna 1.

Je třeba připomenout, že faktorové zátěže aij jsou pouze odhady skutečných faktorových zátěží.
Je žádoucí, aby komunality nabývaly pokud možno hodnot blízkých 1. To pak svědčí o tom, že je jejich variabilita z velké míry vysvětlena faktorovou analýzou. Část variability proměnné Xi, která nemá vztah k faktorům, Var(ei), se nazývá jedinečnost. Jestliže byla proměnná Xi před zpracováním standardizována, platí, že

komunalita + jedinečnost = 1.

V souvislosti s faktorovou analýzou se také setkáváme s pojmem redukovaná korelační matice. Je to vlastně korelační matice původních proměnných, na jejíž diagonále jsou jedničky nahrazeny komunalitami.
Jak nejlépe dosáhnout toho, aby komunality dosahovaly maximální možné hodnoty, tj. hodnoty blízké jedné? Teoreticky toho lze dosáhnout tím, že počet faktorů bude roven počtu manifestních proměnných. V tomto případě bude mít pro m = k soustava lineárních rovnic jednoznačné řešení, tj. k manifestních proměnných bude převedeno na stejný počet faktorů, jedinečnosti ei budou nulové, nedojde k žádné ztrátě informace a všechny komunality budou rovny jedné. Stejný počet faktorů jako původních proměnných je ale v rozporu s hlavním cílem faktorové analýzy, že počet faktorů má být menší než počet původních proměnných, jinými slovy, že dojde k redukci proměnných. I kdybychom tohoto cíle nedbali, bylo by plýtváním času snažit se převádět pozorované proměnné na stejný počet jiných proměnných, o jejichž významu by bylo možné pouze spekulovat. Tím se dostáváme k jedné z nejtěžších úloh faktorové analýzy - stanovení počtu faktorů. Jde vlastně o hledání kompromisu, přičemž na jedné straně platí, že čím více faktorů se vypočítá, tím větší procento rozptylu proměnných je vysvětleno. Na druhé straně smyslem faktorové analýzy je nalézt pokud možno co nejmenší přijatelný počet faktorů. Proto je třeba počet hledaných faktorů určovat na základě konkrétních dat. Existuje tu několik možností.

Stanovení počtu faktorů

Poměrně nejjednodušší případ nastává, pokud můžeme na základě znalosti zkoumané látky použít teoretický předpoklad o počtu faktorů. Například u testu inteligence předpoklad o existenci čtyř oblastí kognitivních schopností. Počet faktorů pak stanovíme roven 4.

Další možnosti využívají porovnávání rozptylu faktorů s rozptylem manifestních proměnných (tzv. Kaiserovo pravidlo). Protože manifestní proměnné bývají standardizovány, jde vlastně o porovnání rozptylu faktorů s hodnotou 1. Do faktorové analýzy jsou zahrnuty ty faktory, jejichž rozptyl je větší než 1. Pokud analyzujeme kovarianční matici, je variantou této metody neuvažovat ty hlavní komponenty, jejichž rozptyl je menší než průměrná hodnota z rozptylů všech faktorů. Na tomto místě je pro úplnost poznamenat, že rozptyl faktoru lze matematicky určit jako vlastní číslo kovarianční či korelační matice.

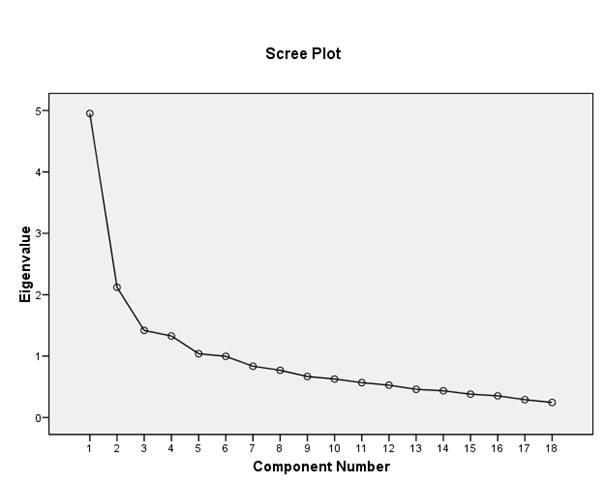
Grafickou metodou pro stanovení počtu faktorů je sutinový graf, známý též jako scree plot. Jedná se vlastně o graf vlastních čísel (rozptylů) všech faktorů. Křivka grafu je klesající a mez oddělující vhodný počet faktorů nacházíme tam, kde vidíme nejvyšší pokles vlastních čísel mezi dvěma faktory. Na obr. 1 vidíme, že pokud se nechceme omezit na jeden nebo dva faktory, dochází k většímu poklesu grafu až zase mezi čtvrtým a pátým faktorem. Proto bude vhodné se omezit na 4 faktory.

Obr. 1 Sutinový graf

Metody extrakce faktorů

Metody extrakce faktorů jsou vlastně metodami, jak určit počet faktorů a velikost faktorových zátěží, jinými slovy, jak na základě výběru n osob z určitého základního souboru nejlépe odhadnout k.m faktorových zátěží aij (faktorovou matici) a k jedinečnosti ei.

Metoda hlavních komponent (principal component ) dává nekorelované faktory, které jsou navíc uspořádány podle svého rozptylu, a to tak, že první faktor má rozptyl největší a poslední nejmenší. Metoda hlavních komponent existuje i samostatně, faktorovou analýzu lze považovat za její rozšíření. Zatímco analýza hlavních komponent se snaží redukovat počet proměnných tak, aby byl co nejlépe objasněn rozptyl původních proměnných, faktorová analýza se pokouší objasnit co nejlépe korelace původních proměnných. Výpočet faktorových zátěží metodou hlavních je jednoznačný, a pokud zvýšíme počet faktorů (komponent), původní komponenty se nezmění. To u ostatních metod extrakce neplatí.

První hlavní komponenta se určuje jako lineární kombinace manifestních proměnných, která má co největší variabilitu za podmínky, že součet druhých mocnin korelačních koeficientů je roven 1. Splnění této podmínky se vyžaduje proto, aby nebylo možné zvětšovat rozptyl pouhým navýšením faktorových zátěží.

áhlavní komponenta se obdobně vypočte jako lineární kombinace manifestních proměnných, která má co největší variabilitu za podmínky, že součet druhých mocnin korelačních koeficientů je roven 1, a která je nekorelovaná s první hlavní komponentou. Tímto způsobem lze získat z k manifestních proměnných k hlavních komponent.
Matematicky lze tento postup popsat jako iterační postup vedoucí ke stanovení m největších vlastních čísel korelační matice a jim odpovídajících vlastních vektorů.

V případě vysokých korelací mezi proměnnými je možné celkový rozptyl zachytit pouze jednou hlavní komponentou. Naopak v případě korelací blízkých nule potřebujeme k vysvětlení celkového rozptylu tolik hlavních komponent, kolik je manifestních proměnných. Rovnice pro vyjádření hlavních komponent pomocí manifestních proměnných se dají obrátit a původní proměnné vyjádřit pomocí hlavních komponent. Přitom lze komponenty s malými rozptyly zanedbat.

Metoda hlavních komponent má tu výhodu, že dává jednoznačné faktorové řešení, kde latentní proměnné vyčerpávají nejvyšší možné procento rozptylu. Proto tato metoda patří mezi nejčastěji používané. Odpůrci této metody namítají, že není metodou, která by nejlépe vysvětlovala korelace manifestních proměnných. 

Metoda hlavních os (principal-axis) je obdobná metodě hlavních komponent s tím rozdílem, že je matice výběrových korelačních koeficientů nahrazena redukovanou korelační maticí.

Metoda nejmenších čtverců
Faktory jsou extrahovány tak, aby byl minimalizován součet čtverců reziduálních korelačních koeficientů, které neleží na diagonále korelační matice.

Zobecněná metoda nejmenších čtverců
Metoda extrakce faktorů je obdobná metodě nejmenších čtverců. Faktory jsou extrahovány tak, aby byl minimalizován součet čtverců reziduálních korelačních koeficientů, které neleží na diagonále korelační matice. Reziduální korelační koeficienty jsou přitom převáženy tak, že korelace proměnných, které mají vyšší jedinečnosti mají nižší váhu než korelace proměnných s nižšími jedinečnostmi.

Metoda maximální věrohodnosti
Odhad metodou maximální věrohodnosti je velmi rozšířený postup, který za předpokladu normálního rozdělení většinou vede ke stejným výsledkům jako metoda nejmenších čtverců. K pochopení této metody je třeba si uvědomit, že postup faktorové analýzy nerealizujeme na zkoumaném základním souboru, ale pouze na výběru z tohoto souboru.  Proto musíme rozlišovat tři typy pojmů. Za prvé to jsou neznámé korelační koeficienty v základním souboru, ke kterým přísluší i neznámé faktorové zátěže a jedinečnosti. Za druhé to jsou jejich odhady a za třetí konkrétní odhady provedené na daném výběru, především výběrové korelační koeficienty rij.

Základní myšlenka metody maximální věrohodnosti je odhadnout takové parametry základního souboru, pro které je pravděpodobnost, že se vyskytnou u našeho výběrového souboru, největší. Základem výpočtu je při metodě maximální věrohodnosti určení  věrohodnostní funkce. Ta se stanoví jako pravděpodobnost výskytu našeho výběru v závislosti na hodnotách parametrů základního souboru. Parametry, pro které nabývá věrohodnostní funkce maxima, jsou maximálně věrohodné odhady.

Pro ověření adekvátnosti modelu se konstruuje věrohodnostní poměr λ, který je mírou "neshody" odhadu parametrů s danou výběrovou korelační maticí. Tato míra vyjadřuje, nakolik se reziduální korelační koeficienty blíží nule.  Pokud je splněn předpoklad normality zkoumaných dat a výběrový soubor je velký, lze navíc dokázat, že věrohodnostní poměr λ má rozdělení χ2 (chí kvadrát) s počtem stupňů volnosti

df = ½ [(k - m)2 - (k + m)].

Pokud nemůžeme zamítnout hypotézu o neshodě matic (siginifikance je větší než 5%)  model odpovídá datům. V opačném případě je třeba model rozšířit o další faktory. Test má velkou nevýhodu, že závisí na počtu pozorování, s rostoucí velikostí analyzovaného souboru se i malé neshody stávají statisticky významnými a test zamítá i jinak správný model. Test je tedy třeba používat pouze jako doplněk analýzy a jeho použití se omezuje na menší soubory.

Metoda alpha předpokládá, že proměnné, ne případy pocházejí z výběru.

Image factoring - společná část proměnné je definována jako lineární regrese zbývajících proměnných.

Rotace faktorů

Bez ohledu na metodu extrakce faktorů existuje nekonečně mnoho faktorových řešení. Znamená to, že ke každému odhadu faktorových zátěží existuje nekonečně mnoho dalších alternativ, které vystihují data stejně dobře. Proto se ve druhé fázi faktorové analýzy faktory transformují tak, abychom je mohli co nejlépe interpretovat. Praxe přitom ukázala, že nejlépe se interpretují takové faktory, jejichž faktorové zátěže nabývají hodnot blízkých buď jedné, nebo nule. To znamená, že každá manifestní proměnná je silně korelována jen s některými faktory a s ostatními faktory je korelována slabě. Tato fáze faktorové analýzy se nazývá rotace faktorů. Název "rotace" se ujal proto, že pro 2 faktory si tuto operaci můžeme představit jako pootočení, tj. rotaci souřadnicových os.  To lze ilustrovat např. na následujícím příkladu:
Představme si faktorové řešení ve tvaru

X1  =   0,5 F1  +  0,5 F2
X2  =   0,5 F1  –  0,4 F2
X3  =   0,7 F1  +  0,6 F2
X4  =  -0,6 F1  +  0,5 F2

Toto faktorové řešení je zobrazeno na obr. 2. Souřadnicové osy F1 a F2  jsou zobrazeny černě, původní faktorové zátěže zeleně.  Pootočíme-li faktory F1 a F2 o 45˚, získáme nové souřadnicové osy F1'  a F2', faktorové zátěže jsou po rotaci označeny oranžově. Vidíme, že po rotaci skutečně došlo k tomu, že některé faktorové zátěže jsou prakticky nulové nebo nule blízké. Rotované faktorové řešení má přibližně tvar

X1  =   0,71 F1'  +  0,00 F2'
X2  =   0,07 F1'  –  0,58 F2'
X3  =   0,92 F1'  –  0,07 F2'
X4  =  -0,08 F1'  +  0,78 F2'

Obr. 2

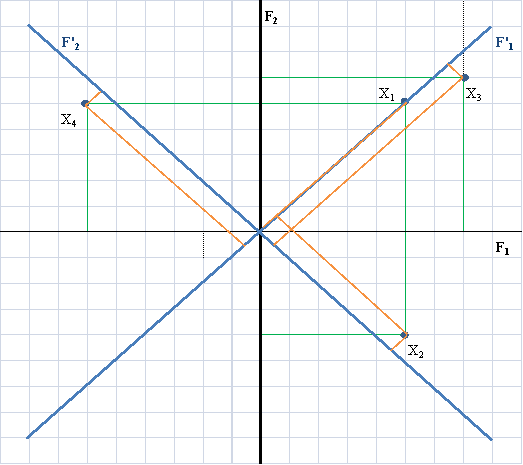
Vidíme, že první faktor je po rotaci sycen pouze proměnnými X1 a X3, druhý pak X2 a X4. Přitom před rotací byly oba faktory syceny všemi čtyřmi proměnnými.

Pojem rotace úzce souvisí s představou jednoduché struktury matice faktorových zátěží. Matice faktorových zátěží má jednoduchou strukturu když:
- Každý řádek obsahuje nejméně jednu zátěž blízkou nule.
- Každý sloupec obsahuje nejméně tolik malých zátěží, kolik je faktorů.
- Pro každou dvojici sloupců existuje alespoň tolik dvojic proměnných, z nichž jedna má malou zátěž u jednoho faktoru a druhá velkou zátěž u druhého faktoru, kolik je společných faktorů.

Tato definice jednoduché struktury matice zátěží není přesná, protože v ní není specifikováno, co je to faktorová zátěž blízká nule, malá a velká. V praxi ale s touto definicí vystačíme. Pokud bychom se pohybovali v teoretické rovině, musely by být výrazy "blízká nule" a "malá" nahrazeny slovem "nulová" a výraz "velká" slovem nenulová. V praxi ale těžko získáme nulové faktorové zátěže.

Zvykem je uvažovat faktorové zátěže v absolutní hodnotě menší než 0,3 jako „blízké nule“, a za „velké“ uvažovat faktorové zátěže v absolutní hodnotě větší než 0,5. Faktorová zátěž rovna 1 znamená, že daná proměnná je zcela nasycena daným faktorem, tj. jde o faktorově čistou proměnnou. Faktorová zátěž rovna 0 ukazuje, že proměnná není daným faktorem vůbec dotčena.

Zvláštním případem jednoduché struktury matice faktorových zátěží jsou nezávislé shluky, kdy každá proměnná má nenulovou zátěž pouze u jednoho faktoru. Princip jednoduché struktury matice faktorových zátěží zdůvodnil Thurstone tím, že k řešení kognitivních úloh nepoužíváme všechny naše schopnosti současně. Přijatelnost požadavku jednoduché struktury je tedy možná dána spíše způsobem lidského myšlení než povahou zkoumaných dat.

Pro rotaci faktorů bylo navrženo mnoho metod, z nichž většina je založena na tzv. simplicitní funkci, která je funkcí všech prvků matice faktorových zátěží. Ta je zkonstruována tak, aby nabývala maxima nebo minima při přiměřené aproximaci jednoduché struktury. Bylo vytvořeno několik variant simplicitních funkcí, přičemž metody na nich založené dávajících odlišná řešení. Nadto je těžké stanovit, která implicitní funkce je obecně nejlepší. Zůstává proto jenom na výzkumníkovi, kterou z metod použije. Rozhodování má přitom několik fází.

Prvním krokem je rozhodnutí mezi pravoúhlou (ortogonální) a šikmou rotací. Pravoúhlou rotaci si můžeme představit jako pootočení všech os o stejný úhel, což poskytne řešení s nekorelovanými faktory. Hlavním důvodem pro použití ortogonální rotace je pojetí, ve kterém se předpokládá, že latentní proměnné by měly být  jakési základní, nezávislé, a tedy i nekorelované proměnné.

V šikmém řešení dostáváme faktory korelované, což mnohdy lépe odpovídá realitě. Například testy kognitivních schopností mají tendenci spolu kladně korelovat a poskytovat jeden generální faktor - všeobecnou inteligenci. U kosé rotace je ale situace komplikovanější, můžeme získat dvě matice faktorových zátěží – jednak tzv. faktorový vzor, obsahující regresní koeficienty proměnných na faktorech, jednak tzv. faktorovou strukturu, která obsahuje koeficienty korelace. Při ortogonální rotaci jsou tyto dvě matice totožné.  Pro interpretaci faktorů u šikmé rotace používáme matici faktorové struktury.
Jednotlivé metody rotace popíšeme v pořadí od nejčastěji používaných (a pro interpretaci faktorů nejméně záludných).

Varimax je ortogonální rotace, která minimalizuje počet proměnných, které mají vysoké zátěže s každým společným faktorem. Lze o ní mluvit jako o metodě zjednodušující faktory. Simplicitní funkce tu je dána součtem rozptylů čtverců faktorových zátěží v jednotlivých sloupcích. Protože faktory s malým počtem vysokých zátěží u proměnných se snáze interpretují, je tato metoda nejvhodnější pro začátečníky, protože pro interpretaci faktorů vyžaduje relativně nejmenší zkušenosti. Tato metoda má tendenci nevytvářet jeden všeobecný faktor.

Quartimax je ortogonální rotace, která minimalizuje počet faktorů, kterých je potřeba pro vysvětlení jednotlivých proměnných. Simplicitní funkce tu je dána součtem rozptylů čtverců faktorových zátěží v jednotlivých řádcích. Lze o ní mluvit jako o metodě zjednodušující proměnné, má tedy tendenci ponechávat jeden všeobecný faktor.

Equamax je kombinace metody Varimax a Quartimax. Je při ní minimalizován jak počet proměnných, které mají vysoké zátěže s každým společným faktorem, tak počet faktorů, kterých je potřeba pro vysvětlení jednotlivých proměnných. Jedná se o ortogonální rotaci.

Oblimin je šikmá rotace pomocí které se dosahuje jednodušší struktury faktorů než by bylo možné u ortogonální rotace. Využívá se především tam, kde z povahy zkoumaných dat a výsledných faktorů je zřejmé, že faktory pravděpodobně nemohou být nezávislé.

Promax je šikmá rotace, vhodná pro stejný typ dat a faktorů jako metoda oblimin. Na rozdíl od metody oblimin je rychlejší, proto se používá především pro velké soubory dat.

Příklad jednoho z možných faktorových řešení udává tabulka 2.

Tab.2 Faktorové zátěže získané metodou maximální věrohodnosti a rotací varimax

	Component
	1	2	3	4
01 Žít ve správně rodině	,471
02 Žít ve zdravém životním prostředí		,546
03 Být vzdělaný, mít velké znalosti		,609
04 Hodně cestovat, poznávat různé země
05 Pomáhat všude, kde je potřeba	,513	,324
06 Dobře vypadat, mít pěkný osobní vzhled			,506
07 Umět se o sebe postarat, být samostatný				,587
08 Být ve svém budoucím životě úspěšný			,632
09 Umět se prosadit, mít dobré nápady			,460
10 Žít v blahobytu, mít hodně peněz			,642
11 Žít ve shodě se svojí náboženskou vírou				-,309
12 Mít pocit, že jsem někomu užitečný	,483	,315
13 Najít si dobrého životního partnera	,730			,418
14 Být tolerantní, žít v dobrém vztahu s lidmi	,717
15 Být hrdý na zemi, kde jsem se narodil	,438	,468
16 Naučit se poctivě pracovat,odevzdávat co nejlepší výkon	,576	,645
17 Chovat se vždy tak, aby si mne lidé vážili	,810
18 Nemít velké zdravotní problémy	,407
Extraction Method: Maximum Likelihood Rotation Method: Varimax with Kaiser Normalization.
a  Rotation converged in12 iterations.

Matice rotovaných faktorových zátěží bývá následována maticí koeficientů dij, které udávají podobu konkrétní lineární transformace vedoucí k převodu původních faktorů Fi na rotované faktory Fi'. Pro koeficienty dij platí

Fi' = di1 F1 + di2 F2 + di3 F3 +      + dim Fm

pro i = 1, 2, 3, … m.