Korelační analýza

Cílem korelační analýzy je určit sílu lineární závislosti mezi veličinami. První představu o závislosti znaků X a Y lze získat tak, že tyto znaky sledujeme u n statistických jednotek a zjištěná data znázorníme bodovým diagramem. Je to diagram, v němž je každá dvojice pozorování (x_i,y_i) znázorněna jako bod v pravoúhlé souřadnicové soustavě, kde na vodorovné ose je umístěna stupnice hodnot znaku X a na svislé stupnice hodnot znaku Y. Vynesené body pak tvoří množinu, z níž lze vystopovat charakteristické rysy závislosti obou znaků.

Bodový diagram pro posouzení závislosti potřeby úspěšného výkonu (PUV) a prospěchu žáků.

Pearsonův korelační koeficient

Nejčastěji se pro měření závislosti používá Pearsonův korelační koeficient r , který měří lineární závislost dvou náhodných veličin s dvourozměrným normálním rozdělením

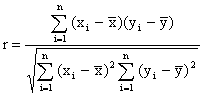
Součty čtverců ve jmenovateli jsou n-1 násobkem výběrových rozptylů. Proto se často setkáváme s jednodušším vyjádřením korelačního koeficientu

r = ,

kde s_x je směrodatná odchylka proměnné X, s_y směrodatná odchylka proměnné Y a s_xy takzvaná kovariance proměnných X a Y

s_xy = .

Správná interpretace korelačního koeficientu předpokládá, že obě proměnné jsou náhodné veličiny a mají společné dvourozměrné normální rozdělení. Potom nulový korelační koeficient znamená, že veličiny jsou nezávislé. Pokud není splněn předpoklad dvourozměrné normality, z nulové hodnoty korelačního koeficientu nelze usuzovat na nic víc, než že veličiny jsou nekorelované.

Čím těsnější je vztah mezi oběma veličinami, tím více se absolutní hodnota korelačního koeficientu blíží k jedné. Záporné hodnoty korelačního koeficientu vyjadřují nepřímou korelaci (se zvyšováním hodnot jedné proměnné se snižují hodnoty druhé proměnné - např. čím vyšší počet bodů v didaktickém testu, tím lepší (nižší) známka), kladné hodnoty udávají korelaci přímou (se zvyšováním hodnot jedné proměnné se zvyšují i hodnoty druhé proměnné - např. čím delší období přípravy k testu, tím vyšší bodové ohodnocení).

Druhá mocnina korelačního koeficientu se nazývá koeficient determinace. Vyjadřuje podíl, jakým je rozptyl závisle proměnné veličiny vysvětlen změnami nezávisle proměnné. Obvykle se násobí stem, čímž je podíl, jakým je rozptyl závisle proměnné veličiny vysvětlen změnami nezávisle proměnné, vyjádřen v procentech.

Korelační matice

Různé praktické důvody, ale zejména potřeba vyjádřit se současně o větším počtu proměnných, např. o prospěchu žáka v různých předmětech, vedou často k vícerozměrnému přístupu ke korelační analýze. Při současném zpracování n proměnných hodnotíme korelační koeficienty n(n-1)/2 dvojic proměnných, které sestavujeme do korelační matice, jejíž řádky
i sloupce jsou věnovány postupně první až n-té proměnné. Na průsečíku i-tého řádku a j-tého sloupce je tedy uveden korelační koeficient r_ij i-té a j-té proměnné. Korelační matice je čtvercová a na diagonále obsahuje jedničky, protože r_ii = 1.

Korelační matice pro průměrný prospěch, PUV (potřeba úspěšného výkonu) a PVN (potřeba vyhnout se neúspěchu)

Correlations

		Průměrný prospěch	PUV	PVN
Průměrný prospěch	Pearson Correlation	1	-,478(**)	,164(**)
	Sig. (1-tailed)		,000	,001
	N	478	387	387
PUV	Pearson Correlation	-,478(**)	1	-,261(**)
	Sig. (1-tailed)	,000		,000
	N	387	388	388
PVN	Pearson Correlation	,164(**)	-,261(**)	1
	Sig. (1-tailed)	,001	,000
	N	387	388	388

** Correlation is significant at the 0.01 level (1-tailed).

T-test pro korelační koeficient

Zpravidla nezjišťujeme korelační koeficient u celé sledované populace, ale odhadujeme ho na výběru. Potom je třeba provést statistický test nulové hypotézy, která tvrdí, že výběr pochází z dvourozměrného normálního rozdělení, v němž je korelační koeficient nulový. Za platnosti H₀ má veličina

rozdělení t o n - 2 stupních volnosti, kde n je rozsah výběru.

Tento vzorec se ale nehodí pro test hypotézy rovnosti korelačního koeficientu nenulové hodnotě. Proto je třeba hodnotu r pomocí vhodné transformace "normalizovat".

Fisherova transformace

Nejpoužívanější transformace je dána logaritmickým vztahem

.

Hodnoty z mají pro velký počet pozorování přibližně normální rozložení bez ohledu na to, jak velký je korelační koeficient. Výběrová chyba veličiny z má jednoduchý tvar

.

Pro test hypotézy r = r₀ pak použijeme testové kritérium U

U = (z - z₀) ,

přičemž z₀ získáme pomocí výše uvedené transformace kde za r dosadíme r₀. Chceme-li testovat hypotézu o shodě dvou nebo více korelačních koeficientů postupujeme obdobně.

Při tvorbě obecných výroků vztahujících se souběžně k většímu počtu proměnných je třeba zachovat určitou opatrnost. Ve stručnosti lze říci, že tu nestačí prostě kombinovat úsudky o jednotlivých dvojicích proměnných, protože kombinovaný výrok by měl už podstatně nižší spolehlivost. Pro řešení takových úloh lze doporučit některé z metod vícerozměrné statistické analýzy, kterým je věnována např. kniha (Anděl, J. 1978).

Spearmanův korelační koeficient

Pearsonův korelační koeficient daný vztahem lze použít i pro pořadové proměnné, jsou-li pořadová čísla brána jako naměřené hodnoty. Dá se dokázat, že za těchto okolností vzorec pro Pearsonův korelační koeficient přechází do jednoduššího tvaru

r = 1 - ,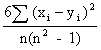

který se nazývá Spearmanův koeficient korelace.

Interval spolehlivosti pro korelační koeficient

Pro konstrukci intervalu spolehlivosti použijeme Fisherovu transformaci. Pak platí

P (-u_1-a/2 < (Z - z₀) < u_1-a/2) = 1 - a.

Odtud lze zjistit, že pro konkrétní hodnotu z (vypočtenou pro daný korelační koeficient) platí

P (Z - u_1-a/2< z₀ < Z + u_1-a/2) = 1 - a.

Dvoustranný 100(1-a)procentní interval spolehlivosti je tudíž

(z - u_1-a/2, z + u_1-a/2).

Ze vztahu

lze odvodit, že

.

Pomocí této transformace lze meze spolehlivosti pro z převést na meze spolehlivosti pro korelační koeficient.

Mnohonásobný koeficient korelace

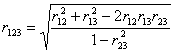
Parciální korelační koeficient

.

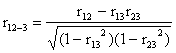Pro test významnosti koeficientu parciální korelace se dá použít podobného vzorce jako pro Pearsonův koeficient korelace, ovšem máme přitom o jeden stupeň volnosti méně, a proto

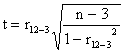
má při platnosti H₀: r_12-3 = 0, t rozdělení s n - 3 stupni volnosti. Rovněž Fisherova transformace je pro parciální korelaci dovolena, přičemž při výpočtu výběrové chyby se hodnota n - 3 sníží na n - 4.

Kendallův koeficient pořadové korelace

,

kde P je počet konkordancí, Q počet diskordancí a n počet pozorování. Přitom platí, že dvě dvojice pořadí pozorování (x_i , y_i) a (x_j, y_j) jsou konkordantní když pro x_i < x_j je y_i <y_j nebo když pro x_i > x_j je y_i > y_j . Naproti tomu dvě dvojice pořadí pozorování (x_i , y_i) a (x_j, y_j) jsou
diskordantní  když pro x_i < x_j je y_i > y_j nebo když pro x_i < x_j je y_i > Ry_j .

Bodově biseriální korelační koeficient

je vztah mezi spojitou metrickou proměnnou a proměnnou binární nabývající hodnot 0,1. Označíme-li spojitou proměnnou y a binární proměnnou x, platí že

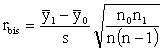
kde je průměr těch y_i , u nichž je x = 1, je průměr těch y_i , u nichž je x = 0, s je výběrová směrodatná odchylka všech y, n₀ je počet nul a n₁ počet jedniček mezi x.

Závislost kvalitativních znaků

Síla závislosti dvou kvalitativních znaků se nejčastěji udává koeficientem kontingence

KK = ,

kde K je hodnota testového kritéria používaného pro test závislosti dvou kvalitativních znaků (viz http://kps.pedf.cuni.cz/skalouda/chi_kvadrat.doc). Nevýhoda koeficientu kontingence KK spočívá v tom, že i při úplné závislosti (v kontingenční tabulce je v každém řádku resp. sloupci obsazeno jedno jediné políčko) je KK menší než 1. Proto se používá oprava

KK_O = ,

kde

KKmax = ,

kde r značí počet řádků v kontingenční tabulce. V tabulkách, které nejsou čtvercové (r ¹ c), je třeba za r dosadit vždy menší z obou hodnot r, c.